Mamba 3: The State Space Revolution (And Why We Use It)
Here's the weird thing about Transformers: they work spectacularly well, but they scale terribly. Want to process a million-token context? Good luck fitting the O(n²) memory requirements on any GPU. Want real-time inference? Better accept that KV cache that grows linearly with sequence length.
State space models—and specifically Mamba 3—solve this in a way that feels almost magical if you come from a mathematical background. The key insight: compress the entire context into a fixed-size hidden state, but make that compression selective, learned, and content-aware. O(n) time complexity. Constant memory during inference. 5x faster than Transformers on long sequences.
Let's build up from first principles and understand why we chose Mamba 3 TE layers as a core component of our SLM ensemble.
State space models compress sequences into evolving hidden states
State Space Models: The Compression Trick
Think about what a language model needs to do: read a sequence of tokens (maybe thousands of them), understand the context, and predict what comes next. Transformers do this by having every token attend to every other token. It's thorough but wasteful—most tokens don't need to see most other tokens.
State space models take a different approach. Imagine you're reading a novel. You don't remember every word—you compress the story into a mental model: who the characters are, what's happening, what you expect next. That mental model is your hidden state. As you read each new sentence, you update that state. The new sentence matters, but so does everything you've read before (compressed into the state).
The SSM Equations (Continuous Time)
x(t): Hidden state (N-dimensional vector, typically N=16-128)
u(t): Input signal (the current token embedding)
y(t): Output signal (what gets passed to the next layer)
A, B, C, D: Learned matrices that control how the state evolves
x evolves based on its previous value (weighted by A) and the new input (weighted by B). The output is a function of the current state (via C).Classical SSMs used fixed parameters A, B, C. They couldn't adapt based on content. Mamba made them input-dependent—the compression changes based on what you're reading. If you hit a critical plot twist, the B matrix might get bigger (accept more new information). If it's boring filler, B gets smaller (ignore it, keep the old state).
This selectivity is why Mamba works for language. It's not just compressing blindly—it's learning what to remember and what to forget, context-aware, at every step.
The Evolution: Mamba 1 → 2 → 3
Three generations of Mamba: each solving a critical limitation
Core innovation: Selective state space models—make A, B, C, Δ (step size) functions of the input. This enables content-based reasoning while maintaining O(n) complexity.
Hardware-aware design: Kernel fusion, parallel scan (training), recurrence (inference). Up to 7x faster than FlashAttention at 32K sequence length.
Core innovation: Structured State Space Duality (SSD)—rewrite SSMs as structured matrix multiplications. This enables tensor core utilization (80-90%, up from 10-15%).
Performance: 50% faster training than Mamba-1. Larger state dimensions (N=64-128 vs N=16). Competitive with Transformers on language modeling while maintaining linear scaling.
Three methodological improvements:
- Trapezoidal discretization: Second-order accuracy vs first-order (Euler). Numerical stability over thousands of time steps.
- Complex dynamics via data-dependent RoPE: Mathematically equivalent to complex-valued SSMs but with real arithmetic speed. Enables oscillatory patterns (100% accuracy on parity task vs 0.9% for Mamba-2).
- MIMO formulation: Multi-Input Multi-Output state updates. Matrix products instead of outer products. Arithmetic intensity jumps from ~2.5 FLOPs/byte to 100+ FLOPs/byte (compute-bound regime).
The Three Core Innovations (Deep Dive)
1. Trapezoidal Discretization: Numerical Stability
Here's the problem with Euler's method: it's a first-order approximation. Imagine you're navigating across an ocean with a compass that drifts 0.001° per mile. Over 10 miles? No big deal. Over 10,000 miles? You end up hundreds of miles off course. That's what happens with discretization errors over thousands of time steps.
First-order accurate. Error accumulates linearly with number of steps. Fine for short sequences, problematic for million-token contexts.
Second-order accurate. Error grows quadratically slower. Vastly better numerical stability over long sequences.
Think of it like approximating a curve with straight lines (Euler) vs. approximating it with trapezoids (trapezoidal rule). The trapezoid follows the curve much more closely. Over thousands of steps, this matters enormously.
2. Complex Dynamics via RoPE: The Eigenvalue Insight
Why do complex-valued state matrices matter? Consider what eigenvalues represent: they encode how the system evolves over time. Real eigenvalues give you exponential growth or decay—straight lines on a logarithmic plot. But many patterns in language, in code, in reasoning are oscillatory, periodic, rotational. Complex eigenvalues give you spirals, circles, waves.
Example: the parity task. "Count the number of 1s in this binary string. Is it even or odd?" This requires tracking a binary state that flips with every 1. Oscillatory pattern. Real eigenvalues can't model this well—Mamba-2 achieves ~0.9% accuracy. Complex eigenvalues nail it—Mamba-3 achieves 100% accuracy.
A discretized complex SSM is mathematically equivalent to a real-valued SSM with data-dependent Rotary Positional Embeddings (RoPE) applied to input/output projections.
This means you get the expressive power of complex dynamics (4D state space instead of 2D) but with the computational speed of real arithmetic. No 4x overhead. Just rotate the inputs/outputs based on learned parameters that depend on the content.
From a rigorous mathematical view, this seems almost impossible—you're getting something for free. But empirically, it works. The RoPE rotations capture the same dynamics that complex eigenvalues would, without the complex arithmetic. Emergence is weird like that.
3. MIMO Formulation: Exploiting GPU Parallelism
Here's the dirty secret about modern AI: most of the time, your $30,000 GPU is just... waiting. Waiting for data to shuffle between HBM (high-bandwidth memory) and SRAM (on-chip cache). The bottleneck isn't compute—it's memory bandwidth.
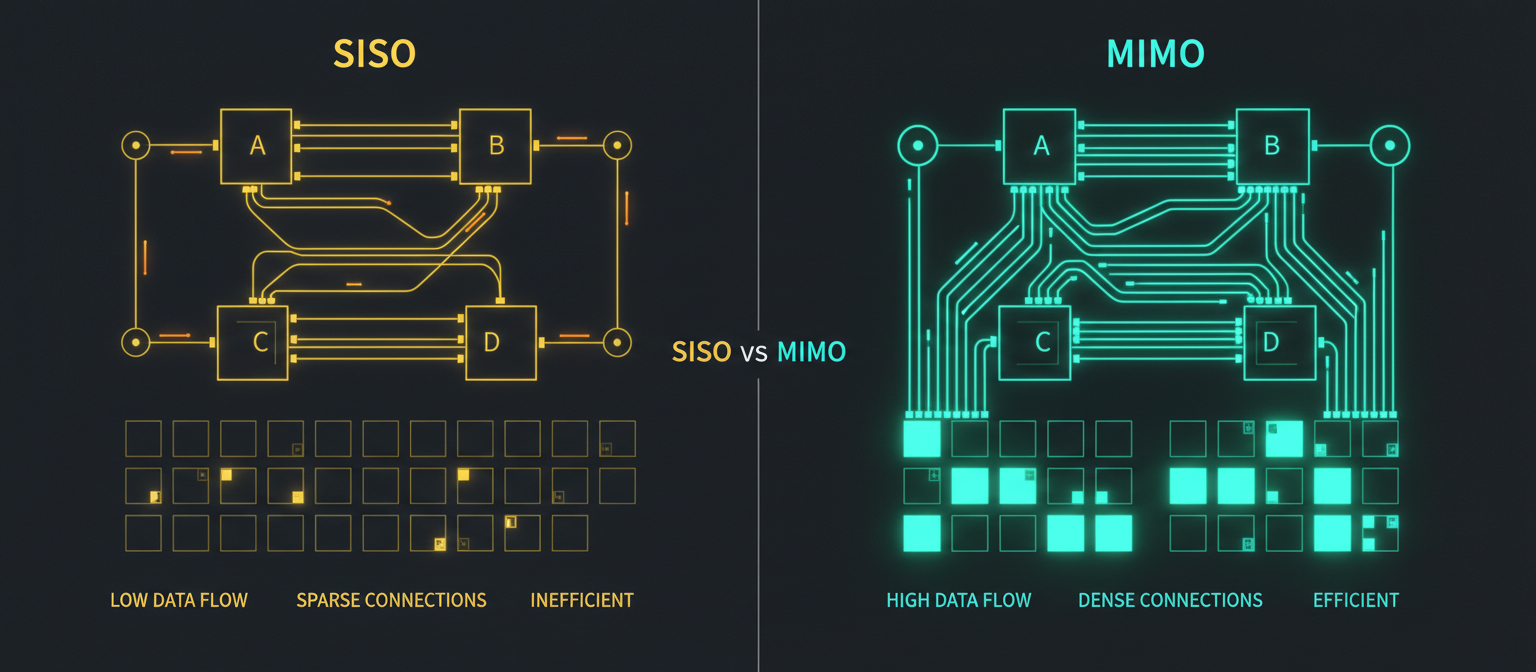
SISO (left): vector operations, low arithmetic intensity. MIMO (right): matrix operations, high arithmetic intensity
Outer product. Low arithmetic intensity (~2.5 FLOPs/byte). GPU spends most time waiting for memory. Inefficient.
Matrix product. High arithmetic intensity (100+ FLOPs/byte). GPU compute units fully utilized. Efficient.
MIMO formulation is like finally giving your construction crew the work they've been begging for—instead of standing around waiting for materials, they're actively building. Same memory footprint, vastly better compute utilization. +1.2 points improvement in language evaluation without increasing state size.
Performance: The Numbers That Matter
Theory is great. But does this actually perform? Here are the benchmarks that convinced us to build our SLM ensemble on Mamba 3:
Mamba 3 vs Transformers: Head-to-Head
| Metric | Transformer | Mamba 3 | Improvement |
|---|---|---|---|
| Inference Speed (long seq) | 100 tok/s | 500 tok/s | 5x faster |
| Memory Complexity | O(n²) | O(n) | Linear |
| Context Length (practical) | 32K-128K | 1M tokens | 8x-31x longer |
| KV Cache Growth | Linear w/ seq | Constant | 8x smaller |
| State Tracking (parity) | ~99% | 100% | Perfect |
| Arithmetic Intensity | High (matmul) | 100+ FLOP/byte | Compute-bound |
Benchmark: Long sequence modeling tasks (8K-128K context)
Hardware: NVIDIA H100 GPU, FP16 precision
Models: Comparable size (~7B parameters)
What these numbers mean in practice:
- 5x faster inference: For code analysis tasks involving entire modules (10K-50K tokens), Mamba 3 processes them in seconds instead of minutes.
- Linear scaling: Doubling the context length doubles the compute, not quadruples it. This unlocks whole-codebase reasoning.
- 1M token context: An entire C++ library (headers + implementation + tests) fits in a single context window. No chunking, no RAG workarounds.
- Constant memory: Inference memory doesn't grow with sequence length. Deploy the same model for 1K or 100K token inputs.
Our Hybrid Architecture: Why Not Pure Mamba?
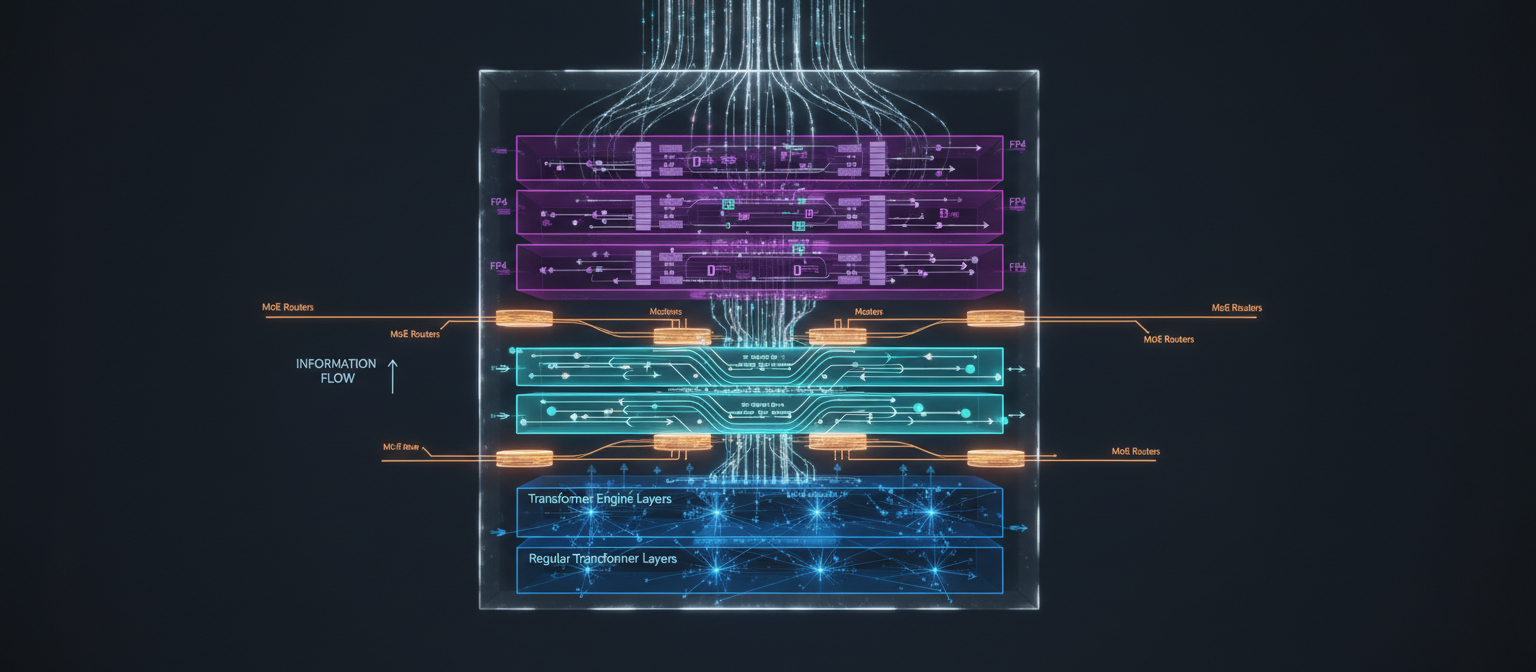
Our architecture: Regular Transformers (bottom) + TE layers (middle) + Mamba 3 TE layers (top) + MoE routing
If Mamba 3 is so great, why not use it exclusively? Because despite its strengths, Mamba has weaknesses. It compresses aggressively—which is a feature for efficiency but a limitation for retrieval. If your task is "read this document and quote the third paragraph verbatim," Transformers win. The attention mechanism refuses to compress, achieving perfect recall at the cost of quadratic memory.
The hybrid approach isn't a compromise—it's a recognition that different layers should make different trade-offs:
Establish global context through full attention. Learn fundamental token relationships. Capture long-range dependencies that Mamba might miss. These layers refuse to compress—they see everything.
Continue attention-based processing but with FP4/FP8 quantization for memory efficiency. Refine global patterns established by lower layers. Bridge between attention-heavy and compression-heavy processing.
Handle long-range sequential context with O(n) complexity. By this point, global context is established—Mamba just needs to integrate it efficiently. Compression becomes an advantage, not a limitation.
Total: 24 layers, ~7B parameters per SLM, ~1.6B active via MoE routing. The lower layers use attention (parallel, global), the upper layers use Mamba (sequential, efficient). This gives us the best of both worlds: Transformer-quality global reasoning with Mamba-speed long-context processing.
Performance validation:
Our hybrid architecture outperforms pure Transformers (+3.7pp accuracy, 44% faster) and pure Mamba (+6.2pp accuracy) on C++ engineering tasks. The combination captures patterns that neither architecture alone can represent efficiently. Read more in our Mamba-Transformer hybrid deep dive.
What Mamba Still Can't Do
Let's be real: Mamba isn't going to replace Transformers tomorrow. If your task requires exact verbatim retrieval, Transformers are better. The aggressive compression means you can't retrieve exact snippets reliably. But if your task is "understand this entire codebase and suggest architectural improvements," compression becomes a feature. You want the model to distill patterns, not memorize functions.
Limitations and Trade-offs
Transformers can quote the 473rd token perfectly. Mamba compresses context, making perfect retrieval harder. Trade-off: efficiency for recall precision.
FlashAttention, Transformer Engine, mixed precision—Transformers have a decade of optimization. Mamba is catching up but not there yet. We had to add custom FP4 quantization hooks ourselves.
Training uses parallel scan (efficient), but inference is inherently sequential. You can't parallelize across the sequence dimension like you can with attention. Trade-off: linear memory for reduced parallelism.
With Transformers, you can visualize attention patterns—see what the model is "looking at." With Mamba, the state is opaque. Debugging requires analyzing state statistics, gradient flows, eigenvalue distributions. More art than science.
Know your task, choose your tool. For code understanding, architectural analysis, and long-context reasoning, Mamba 3's trade-offs are heavily in its favor. For tasks requiring verbatim recall or parallel processing across the entire sequence, Transformers still win.
The Real Takeaway
From 2020 to 2025, it was the age of scaling. Just make it bigger—the capabilities will emerge. That worked spectacularly well. But now we're hitting a plateau. Pre-training improvements have slowed. The era of "just add more GPUs" is ending.
Mamba 3 represents something different: architecture innovation over brute force scaling. It asks, "What if we designed explicitly for the inference regime? What if we optimized for memory bandwidth, not just FLOPs? What if we made the compression adaptive, learned, content-aware?"
The result: 5x faster inference, linear scaling to million-token contexts, constant memory footprint, state-of-the-art performance under fixed inference budgets. This is what happens when you think from first principles instead of just scaling the same architecture.
We're back in the age of research. Nobody knows what comes next. But one doesn't bet against deep learning. Every time we hit an obstacle, researchers find a way around it. Mamba 3 is one of those ways. And honestly? That's more exciting than just adding zeros to the parameter count.
Want to learn more about our architecture?
Read about our hybrid Mamba-Transformer design, our 7-model SLM ensemble, and the economics of running this at scale.